The term “0.06 cubed” refers to the mathematical operation of raising the number 0.06 to the third power. In simpler terms, this means multiplying 0.06 by itself three times. The result of this operation is a small number that can have several practical applications, especially in fields like science, engineering, and mathematics.
Stay tuned with us, We will explore the concept of 0.06 cubed, delve into its mathematical implications, and cover how you can calculate it using different methods. Whether you’re a student learning about cubes and exponents or a professional needing a quick refresher, this comprehensive guide has you covered.
What Is 0.06 Cubed?
To begin with, let’s understand what 0.06 cubed means. In simple terms, 0.06 cubed, written as (0.06)3 involves multiplying the number 0.06 by itself three times:

0.06×0.06×0.06=0.0002160.06
0.06×0.06×0.06=0.0002160.06
This process, known as exponentiation, uses 0.06 as the base and 3 as the exponent, which is why it’s often called “0.06 to the third power.” The result, 0.000216, is a small decimal number. Unlike perfect cubes (like 23 =8),0.06 cubed is an imperfect cube because it includes decimals.
The Cubing And Why It Matters – Learn How To Apply It!
Cubing refers to raising a number to the power of three, which geometrically equates to the volume of a cube with sides of equal length. For instance:
- A cube with side length 1 has a volume of 13=1.
- A cube with a side length of 0.06 has a volume of 0.063=0.000216.
This operation holds importance in:
- Mathematics: It simplifies problems involving volume and exponential growth.
- Engineering: Engineers use cubed values in material science and 3D design.
- Physics: Concepts like density and mass-volume relationships rely on cube calculations.
Latest Post: Depomin82 – Transform Your Digital Experience!
How To Calculate 0.06 Cubed? – A Step-by-Step!
The calculation of 0.0630.06^30.063 is straightforward but requires a careful approach to avoid errors, especially when dealing with decimals. Here’s a breakdown:
First multiplication:
0.06×0.06=0.0036
Second multiplication:
0.0036×0.06=0.000216
Thus, 0.063=0.000216.
To make this process easier, you can also use a scientific calculator or an online tool for cubing any number. For those interested in learning more about exponents, understanding how to manipulate and use powers effectively can be crucial in various areas of mathematics.
Latest Post: Choice Home Warranty George Foreman – Keep Your Home Safe And Secure!
Visualizing the Cube of 0.06 – Understanding Volume in Three Dimensions!
To help you better grasp the concept of cubing a number, let’s imagine a cube in three-dimensional space. If each side of the cube measures 0.06 units, the volume of the cube can be calculated by cubing the side length, which means multiplying 0.06 by itself three times. The formula would look like this:
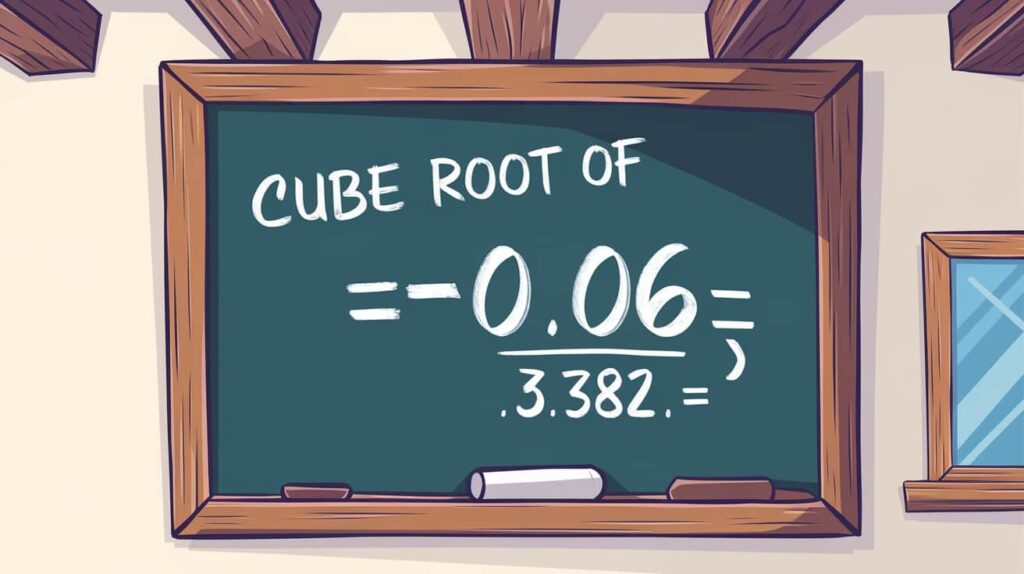
Volume=side length3=0.063=0.000216cubic units
This is a simple and effective way to visualize how “cubing” a number works. It’s just like thinking of a small block or cube with sides measuring 0.06 units. When you multiply the side length by itself three times, you get the volume of the cube. This helps us see how cubing relates to real-world objects, such as small blocks, and how it can be used to understand space and volume.
Properties Of 0.06 Cubed – Discover Its Key Features!
Small Values And Decimals:
One interesting feature of 0.06 cubed is that the result, 0.000216, is quite small. This highlights an important aspect of working with small decimal numbers: as the base number gets smaller, the cube of that number becomes even smaller. This behavior is essential in fields like physics, where measurements often deal with minuscule values.
The Relationship To Other Cubes:
Just as 0.06 has a cube, so do other numbers close to it. For instance, the cubes of 0.055, 0.057, and other nearby values can be calculated, and they gradually increase in value as the base number increases. Here’s a quick look at the cubes of numbers close to 0.06:
| Number | Cube |
| 0.055 | 0.000166375 |
| 0.056 | 0.000175616 |
| 0.057 | 0.000185193 |
| 0.058 | 0.000195112 |
| 0.059 | 0.000205379 |
| 0.06 | 0.000216 |
| 0.061 | 0.000226981 |
| 0.062 | 0.000238328 |
| 0.063 | 0.000250047 |
| 0.064 | 0.000262144 |
Latest Post: Bklis Senior Hearing Aid – Hear Better And Live Better!
Applications of 0.06 Cubed – Explore Its Real-World Uses Now!
While the cube of a small number like 0.06 may seem trivial, it has significant applications in various fields:
Physics And Engineering:
In physics, the cube of a number often represents volume. For example, if you are dealing with a cubic shape where each side has a length of 0.06, the total volume would be 0.063 which is 0.000216 cubic units.
Chemistry:
In chemistry, exponents and cubes are used in calculations related to concentration, molecular structures, and reactions. The cube of a number can represent the volume of particles in a 3D space, which is particularly important when considering the relationship between gas laws and molecule behavior.
Data Science And Technology:
In data science and computing, cubing operations are used in algorithms for processing large data sets. The idea of cube numbers appears when working with 3-dimensional data or multi-dimensional databases, where the data is organized and analyzed in cube-like structures.
The Inverse of Cubing – Cube Root of 0.06!
The inverse of cubing a number is called the cube root. For 0.06, the cube root is the number that, when multiplied by itself three times, equals 0.06. This can be calculated as follows:

Cube Root of 0.06= ∛0.06 ≈0.382
To put it simply, the cube root is the reverse operation of cubing. If you cube a number and then take the cube root of the result, you’ll get back to the original number. This concept is not only important in algebra but also plays a crucial role in higher mathematics, helping solve equations involving cubes and volumes.
How To Calculate Cubes Quickly?
- Use Exponentiation: Simply raise the number to the power of 3 (e.g., 0.06³ = 0.000216) for a faster result.
- Mental Math for Small Numbers: For numbers like 2, 3, or 4, you can cube them in your head (e.g., 2³ = 8).
- Use a Calculator: For decimals or complex numbers, a calculator is the easiest and quickest option.
- Recognize Patterns: With numbers close to each other, you can estimate cubes based on simple patterns.
- Break Down Larger Numbers: For bigger numbers, split them into smaller parts and apply the cube formula.
Latest Post: Ztec100.Com – Simplify Your Health & Insurance Management!
FAQs:
Can I Calculate The Cube Of 0.06 Without A Calculator?
Yes, it’s possible to calculate the cube of 0.06 manually by multiplying 0.06 by itself three times. This involves some basic multiplication, though using a calculator is often quicker and more accurate, especially for decimal numbers.
Is 0.06 Cubed Considered An “Imperfect Cube”?
Yes, 0.06 cubed is an imperfect cube. This is because the result, 0.000216, contains decimals. Perfect cubes are those whose cube roots are whole numbers, but 0.06 has a decimal cube root of approximately 0.382.
Are There Other Ways To Calculate Cubes Besides Using A Calculator?
Yes, besides using a calculator, you can cube numbers manually by multiplying the number three times. Additionally, there are estimation methods for numbers close to whole values, and you can use algebraic methods to solve more complex cube-related problems.
How Does Cubing A Number Affect Its Size?
Cubing a number causes it to grow at a faster rate compared to squaring it. For instance, cubing 0.06 results in 0.000216, a much smaller value than squaring 0.06, which gives 0.0036. Cubing increases the size based on the three dimensions of an object.
Conclusion:
0.06 cubed means multiplying 0.06 by itself three times, which equals 0.000216. This simple operation helps calculate volumes in three dimensions and has practical applications in math, science, and real-life scenarios.
Understanding the concept of cubing allows you to explore relationships between numbers and their spatial representations. Whether done manually or with a calculator, cubing is a valuable mathematical tool. By learning about 0.06³, you gain insights into exponentiation and how it applies to solving everyday problems.
Also Read:




